Passive Apertures

In order to describe the effect of the signal when received by a microphone array, the theory behind transmission/reception of propagating waves needs to be reviewed. An aperture is defined as a spacial region designed to emit (active) or receive (passive) propagating waves. The concept of aperture is very broad and is used for many different kinds of waves.

Figure 2.2: Example of a passive aperture response to different incoming signals

As can be seen in figure 2.2, a passive aperture has a particular spacial orientation in space and therefore alters the receiving signal in a different way for each frequency and location. In this context the aperture function or sensitivity function ( $A(f,\mathbf{r})$, with impulsive response $\alpha(t,\mathbf{r})$) is defined as such response of the aperture to the incoming signal $x(\tau,\mathbf{r}) {\mathcal{F} \atop \Longleftrightarrow} X(f,\mathbf{r})$, resulting on $X_{R}(f,\mathbf{r})$ as

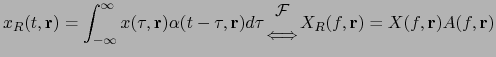$$x_{R}(t,\mathbf{r})=\int_{-\infty}^{\infty} x(\tau,\mathbf{r})\a... ...atop \Longleftrightarrow} X_{R}(f,\mathbf{r}) = X(f,\mathbf{r})A(f,\mathbf{r})$$ (2.26)

The aperture function is defined for a particular direction of arrival. In order to measure and characterize the response of an aperture for all directions, the directivity pattern (or beam pattern) is defined as the aperture response to each frequency and direction of arrival. It is given by:

$$D_{R} (f, \boldsymbol{\alpha} ) = \mathcal{F}_{\mathbf{r}} \{A(f,... ...\infty}A (f, \mathbf{r} )e^{j2\pi \boldsymbol{\alpha} \mathbf{r}} d \mathbf{r}$$ (2.27)

where $\mathcal{F}_{\mathbf{r}}$ is the 3D fourier transform, $\mathbf{r}$ now indicates a point along the aperture and $\boldsymbol{\alpha}$ is the direction vector of the wave

$$\boldsymbol{\alpha}=\frac{1}{\lambda}[\sin\theta \cos\phi \;\; \sin\theta \sin\phi \;\; \cos\theta]$$