Automatic Features Weight Estimation

As seen in equations 5.21 and 5.20, in order to combine the acoustic and TDOA features one needs to determine an optimum set of weights $W_{i}$ that define how relevant each one is. Without an automatic way to determine such value it needs to be found using development data and performing a sweep of the $W_{i}$ parameters optimizing the Diarization Error Rate (DER) score. This constitutes a problem of robustness due to the possible big differences between the development and test sets in terms of the relative importance between features. It also becomes a tedious job if the number of parallel feature streams is big. Some of the factors that reduce the ability of a feature set to optimally represent the speakers in a recording (and therefore its relevance should be reduced) are:

• Acoustics from speakers with very similar voices.

• TDOA values for people very close together.

• TDOA values for people in symmetry with most of the microphones.

• TDOA values in noisy environments (where approximation of the correct TDOA value is difficult) or with multiple impulsive noises.

• TDOA values when the speakers are moving around.

When setting the values by hand they are normally defined for all meetings equally and therefore they do not account for peculiarities due to the meeting room (noisier rooms) or to the nature of the meetings (kind of usual attendees or wether they move from their seats). The automatic weight setting algorithm presented here is able to compute the optimum values for each meeting independently.

Prior art in weights selection for features fusion needs to be searched for in areas other than speaker diarization, like in speaker verification and biometric fusion techniques (Fiérrez-Aguilar et al. (2003), Ross et al. (2001), Verlinde et al. (2000)) and in speech recognition (Misra et al. (2003), Ikbal et al. (2004), Li (2005)). Throughout the literature a well used technique for automatic weighting of different feature streams is based on the feature vectors entropy.

Initial tests were performed using the inverse entropy as relative weight to see how discriminant each feature stream was. This was done by obtaining the weights in a frame-basis via the inverse entropy of the posterior probabilities of the cluster models given the data. For MFCC, PLP and other acoustic features these entropies were comparable to each other and could therefore determine a correct relative weight between features, as shown in Misra et al. (2003). When using it with TDOA values their GMM models are such that low entropy values are obtained for almost every frame, regardless of how accurate the TDOA values can represent a real speaker position.

The proposed technique in this thesis uses the Bayesian Information Criterion (BIC) to compare how well each feature stream differentiates between clusters in order to determine an appropriate stream weighting. The $\Delta$BIC values are independent of the complexity and topology of the models being used and are a good indication of how close two clusters are.

Figure 5.12: First merge cluster-pair BIC values and histogram for acoustic and TDOA features

Given the $\Delta$BIC values between all cluster pairs for the acoustic and TDOA models, figure 5.12 shows the values and their histograms for the meeting EDI_20050216-1051 from the RT06s evaluation data set, computed for all pairs (given 22 initial clusters) for the first iteration of the clustering. The TDOA values are much bigger in average and contain more positive values than the acoustic values. If a weight $W_{1}=0.5$ (equal relevance) is considered, the TDOA BIC values would mask the acoustics and decide which pair to merge, possibly leading to errors as not all the information is considered. In order to allow for different feature streams to contribute in equal conditions in the merging decision it is needed to transform both $\Delta$BIC value sets to have the same scale using the $W_{1}$ weight. This way the TDOA values with overall high $\Delta$BIC are penalized versus the acoustic values in order to be comparable to each other. For a general case of M feature streams, the weight $W_{i}$ assigned to each stream $i$ is defined as

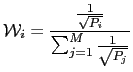$$\mathcal{W}_{i}=\frac{\frac{1}{\sqrt{P_{i}}}}{\sum_{j=1}^{M}\frac{1}{\sqrt{P_{j}}}}$$ (5.22)

where $P_{i}$ is computed from the N $\Delta$BIC values computed for all cluster pairs $x_{j}, x_{k}$ from each feature stream as

$$P_{i} = \frac{1}{N} \sum_{j=1}^{j=N-1} \sum_{k=j+1}^{k=N} \Delta BIC^{2}_{i}(x_{j}, x_{k})$$ (5.23)

This process is equivalent to a variance normalization of single Gaussians modeling each feature stream with zero mean. Setting the mean to zero avoids moving the decision threshold in the $\Delta$BIC comparison, as defined by the BIC theory.

The automatic computation of the $\mathcal{W}_{i}$ weight is performed at the first clustering step, when the $\Delta$BIC values are computed. At the initial segmentation step, no weight has been automatically defined and therefore some initial weight still needs to be determined by hand, or it can be set to an uninformative $\mathcal{W}_{1}= \mathcal{W}_{2} = 0.5$.

On subsequent clustering iterations the models usually represent the clusters better and obtain $\Delta$BIC values which are more accurate. In order to allow the system to refine the weight as the merging iterations progress, the $\Delta$BIC values are kept for all cluster pairs that disappeared during previous iterations and existing pairs are recomputed. Then a new weight is computed taking into account both old and updated values in order to allow for a weight adaptation, containing enough samples for a robust computation.

Figure 5.13: Acoustic weight evolution with the number of iterations for meeting CMU_20050912-0900

To illustrate the effect of the weight adaptation as the system iterates, figure 5.13 shows the evolution of the $W_{i}$ weight over the initial 10 iterations of the algorithm for meeting CMU_20050912-0900 (in the RT06s data set). It is common on all meetings to start with bigger values for the acoustic part and to see it reduced overtime and converging to a final value ( $W_{1} = 0.71$ in this case, converging after 5 iterations). The optimum weight always enhances the acoustic values versus the TDOA values for all shows, both when computed automatically or manually. By doing it automatically each show obtains its own optimum value, which would had been set to $W_{1}=0.9$ manually for RT06s set (including this meeting).

In the experiments section the effect of the number of iterations in which the weight is computed versus the final DER score is computed. It is found that weights always converge to constant values with optimum DER values, therefore leading to a robust solution with one less tuning parameter.